This is a 2 minute (600 word) summary of Epstein SC, Bray TJP, Hall-Craggs MA, Zhang H (2021), Task-driven assessment of experimental designs in diffusion MRI: A computational framework, PLOS ONE 16(10): e0258442.
What is the problem?
MRI is a flexible imaging technique which can exploit a wide range of contrast mechanisms, each one relying on a carefully chosen set of experimental settings.
This presents an optimization problem: selecting the best MR settings for a particular use-case.
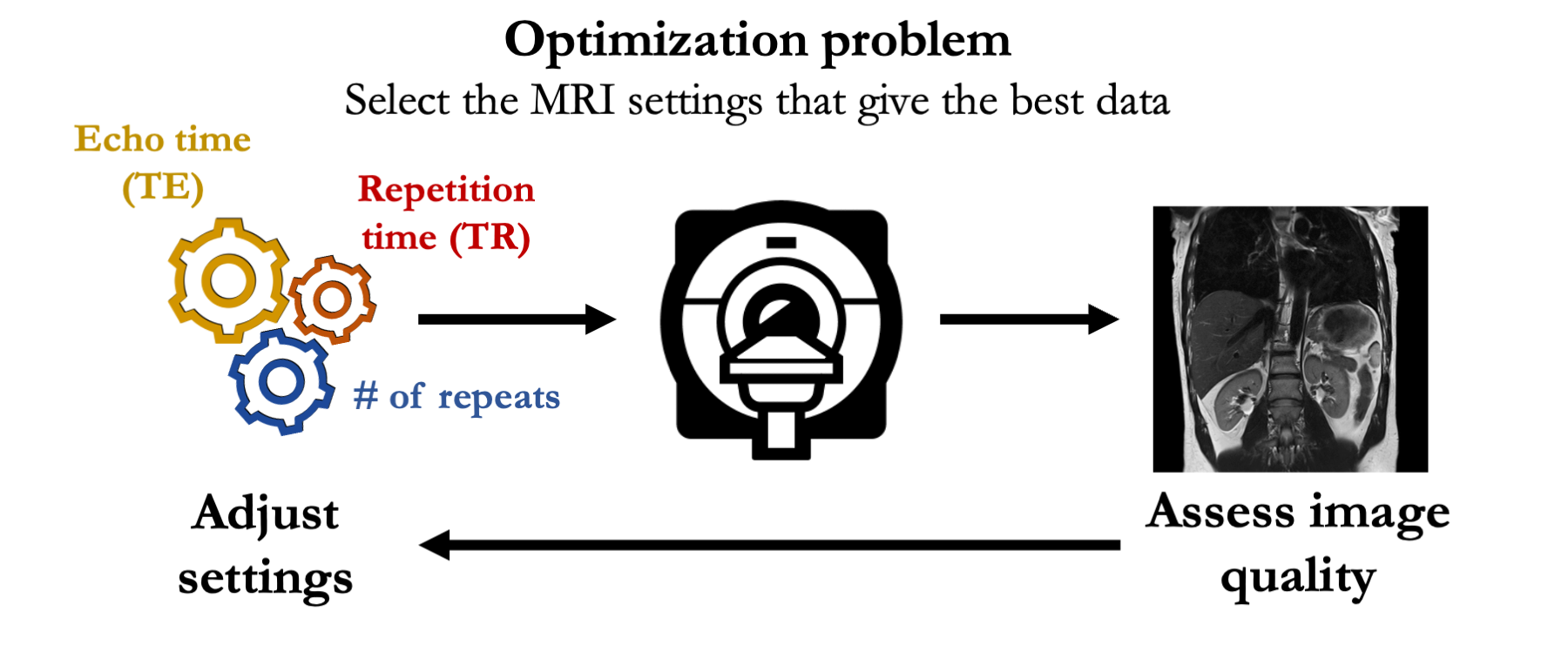Example: determining the MR settings (e.g. echo time) that optimize image quality (e.g. tissue contrast)
Why do we need to solve this computationally?
One way to solve this problem is by brute force: proposing candidate settings, acquiring images with these settings, assessing the resulting images, then going back and adjusting the candidate, each time trying to improve the quality of the associated images. This process is expensive, because the optimization search space is large: there are many possible experimental settings to choose from.
We can make this cheaper by pre-computing a shortlist of high-quality settings, i.e. shrinking the optimization search-space. This is the value offered by computational methods: predicting high quality experimental settings without needing to repeatedly acquire real data.
How do these computational methods work?
In traditional, non quantitative MRI, computational approaches require two components:
- Forward model: a mapping from (a) experimental settings and tissue properties to (b) images
- Objective function: a mapping from (a) images to (b) an assessment metric
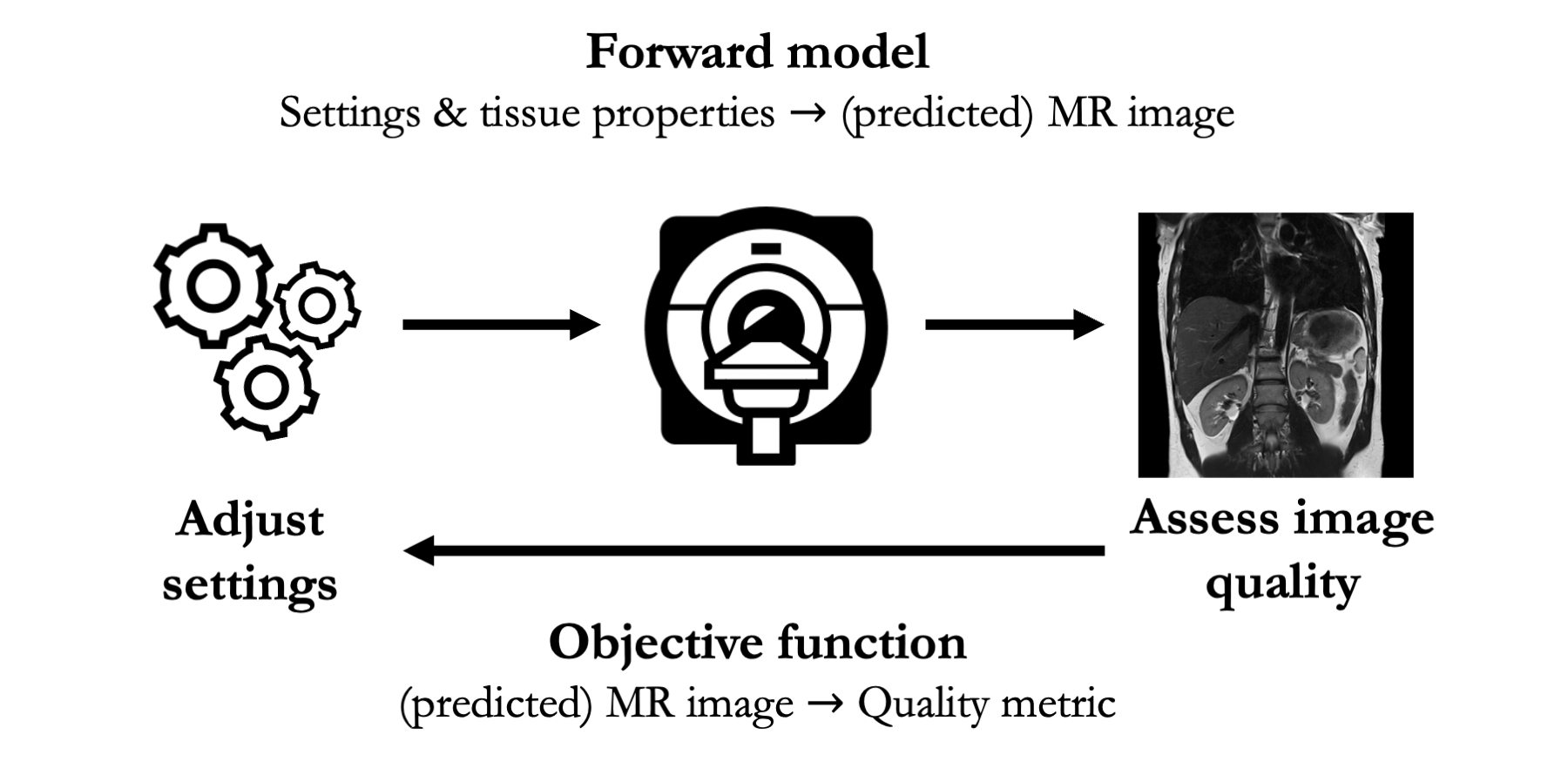
With these two components, computational methods are able to relate MRI settings to associated assessment metrics in silico. This mapping underpins the creation of shortlists of high quality experimental settings.
Why do we need a new approach?
In quantitative MRI (qMRI), this process is more complicated. In these experiments the outputs are not raw images, but rather spatially-dependent biomarkers.
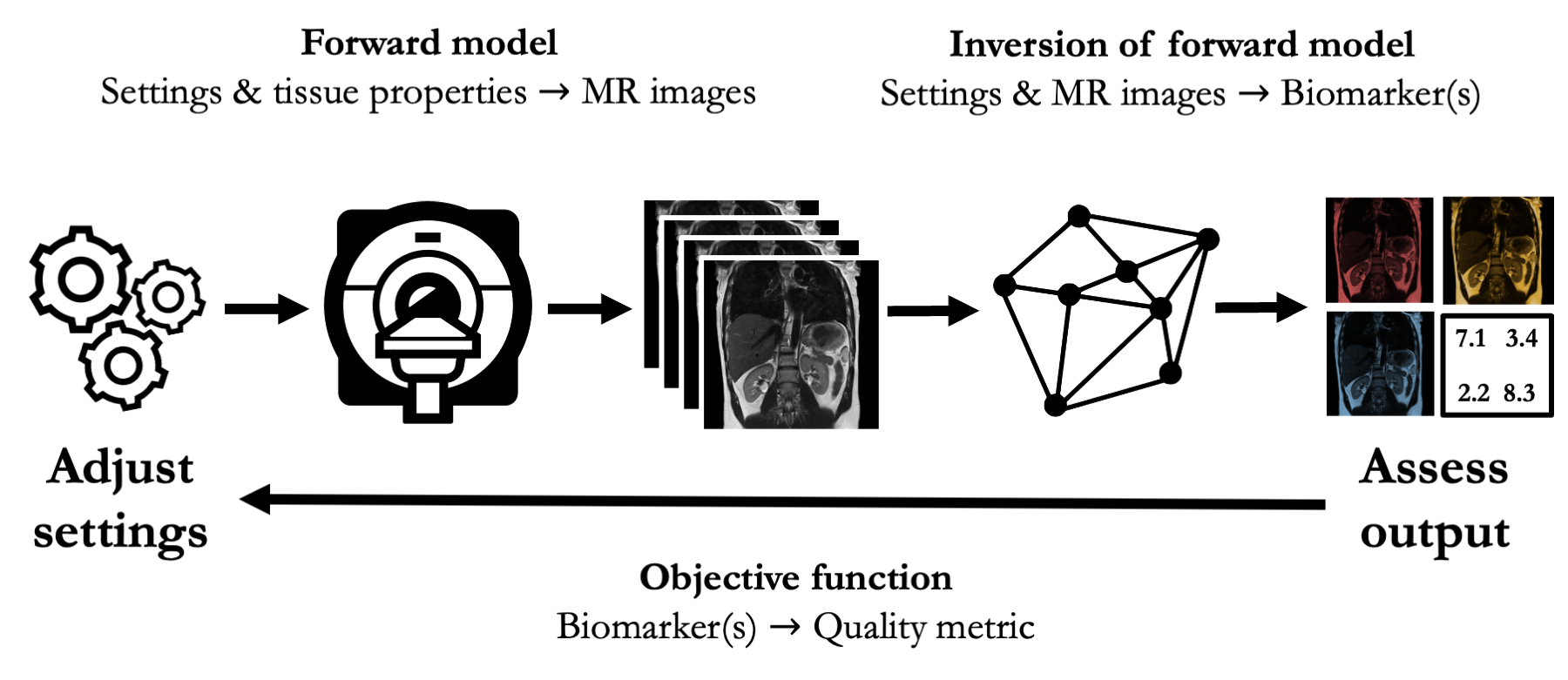
This introduces an inverse problem (model fitting), which presents two complications for computational experimental design.
- The inversion is generally analytically intractable; it is hard to map experimental settings directly to biomarker estimates
- The outputs are biomarkers, not raw images. Each biomarker may be assessed in multiple ways; the choice of objective function is ambiguous.
These complications lead to two limitations of current approaches to computational experimental design (click to expand):
1. Selection of appropriate objective function(s)
Existing methods rely on potentially inappropriate objective functions; they assess experimental settings by comparing their biomarker estimates to groundtruths. For example, in the figure below, traditional objective functions would favour Settings #1 over Settings #2; estimates are numerically closer to groundtruth values.
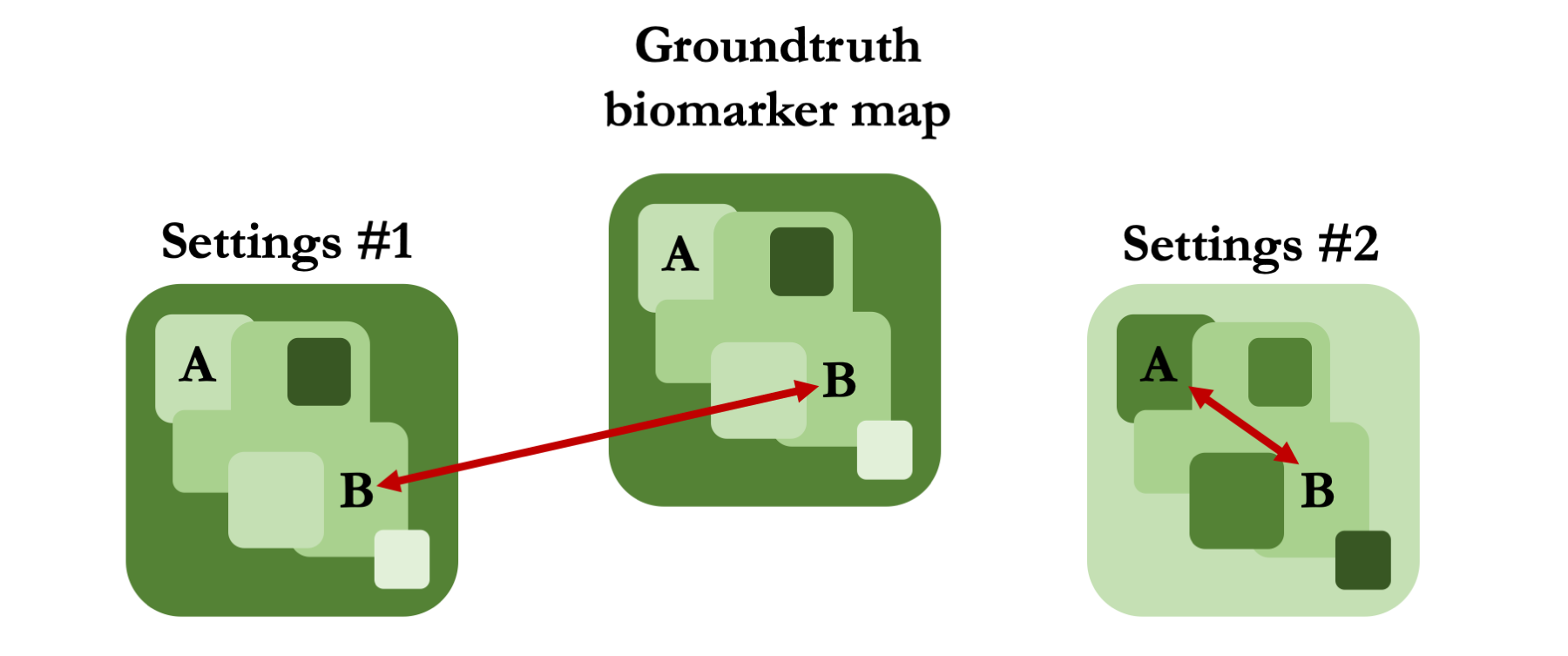
In contrast, we suggest assessing MR settings on their suitability to specific clinical tasks. For example, when distinguishing between tissues A and B, settings #2 would increase utility, despite the associated biomarker estimates being numerically biased.
2. Evaluation of these objective function(s)
Existing methods evaluate and optimize objective functions in an unsatisfactory manner. Since the mapping from settings to biomarkers is generally analytically intractable, it is traditionally broken into chunks (e.g. model selection, data sampling selection), which are assessed and optimized in turn. However, precisely because the mapping is complicated, there is no guarantee that a piecemeal approach gives an overall optimal experiment.
In contrast, we suggest mapping settings to outputs in a holistic way, taking into account the interactions between all parts of an qMRI experiment, despite the associated computational complexity.
What are we proposing?
These limitations motivate the aim of our work:
Developing (and validating) a computational method that maps experimental settings to task performance
Such a method would enable clinicians to tailor qMRI experiments to their needs, whilst minimizing the need for expensive trial-and-error pilot studies.
Our proposed method mimics entire qMRI experiments, beginning to end, in silico. It takes as input a candidate experimental setup, and simulates associated data acquisition, processing, and task evaluation; its final output is resulting task performance.
For further details, including code and validation, see here or get in touch.